 As all FSDO offices do, our local FAA branch office has an accidentprevention program. The fellow who runs it happened to call methe other day to mention that the FAA—ever on the cutting edge—hasjust released a new videotape on loran.
As all FSDO offices do, our local FAA branch office has an accidentprevention program. The fellow who runs it happened to call methe other day to mention that the FAA—ever on the cutting edge—hasjust released a new videotape on loran.
"Great," he says, "now I can show tapes about loranwhen everyone and his brother is interested in this new GPS thingie."
I’m sure the loran tape will be at least as engaging as the circa-1960sVD movies I watched as young a Army trooper. At least it probablywon’t have all those festering open sores. But, my FSDO friendis right. We don’t care about loran anymore. It’s dead meat. We’reAmericans, fer God’s sake and we want new stuff! And that’swhat GPS is. It’s what’s happening in navigation and here, ina nutshell, is how it happens.
Triangulation
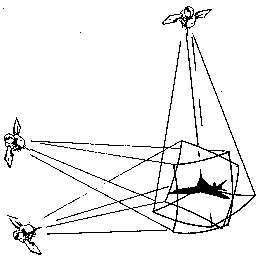 GPS works by triangulation. You remember the concept, right? Backin the stone age, instructors used to send student pilots motoringoff on cross countries with strict instructions to navigate bypilotage and, under no circumstances, to use the VORs. But, justin case they got lost, the students were taught how to triangulatewith crossing radials. In the olden days, students actually followedthe instructions and got lost a lot. They triangulated their wayback to the land of the living, grew up, got out of flying andbecame GPS engineers.
GPS works by triangulation. You remember the concept, right? Backin the stone age, instructors used to send student pilots motoringoff on cross countries with strict instructions to navigate bypilotage and, under no circumstances, to use the VORs. But, justin case they got lost, the students were taught how to triangulatewith crossing radials. In the olden days, students actually followedthe instructions and got lost a lot. They triangulated their wayback to the land of the living, grew up, got out of flying andbecame GPS engineers.
GPS triangulation is different but the principle is the same.Think of triangulation with DME. If you had just DME andno VORs, could you fix your position? Of course! Tune one DMEand draw a circle around it whose diameter equals your distancefrom the station. Tune another DME and do the same. Now you’dhave two intersecting circles that intersect at two points. Yourposition would be at one of those two intersections. If you hadeven a vague idea of where you were, you could throw out the bogusposition and there’d you’d be.
Better, though, is to take a third line of position from yet anotherDME. Now you’d have three intersecting circles and your positionwould be inside the little triangle formed by the intersectionof the three circles.
Got the picture? This is basically how GPS triangulates, exceptinstead of circles, we’re dealing intersecting spheres. And bythe way, there are navigation systems that mix DME informationwith other data (inertial, VOR, etc.) to arrive at a fix. TheFAA’s flight check aircraft use a system that does just that.
Timing’s the thing
Think of GPS satellites as floating DME stations. They move alongin orbit and that complicates things but forget about that forthe moment. How the hell are we gonna measure distance?
Back to DME. You know how it works, right? Your aircraft DME unitis really a transceiver that interrogates a transponder in a VOR-DMEstation. When you tune the DME, your unit sends a signal to theground station, which replies on a different frequency. The receivermultiplies half the total signal transmission time by the speedof light and converts it to distance. Subsequent fixes allow groundspeed and time computations.
GPS does a version of that, but it’s a one-way deal; the satellitestransmit, your receiver listens. And, as we said, the SVs aremoving around up there at about five miles a second, so we haveto account for that, too. You can see how it begins to get complicated.
Like DME, GPS measures the time that it takes the signal to reachthe receiver. However, unlike DME, it doesn’t have benefit ofa returning pulse from an interrogation to act as a baseline.It relies purely on one-way timing. Let’s see here…the satellitesare 10,900 miles up…light (and radio waves) travel at 186,000miles a second so…what?…it’ll take 1/17th of a second forthe signal to reach us.
The math is simple enough. All we need to know is exactly whenthe signal left the satellite. And we do mean exactly.A error of a mere 1/1000th of a second would trash the fix bya factor of 180 miles or so. Obviously, very accurate clocks arerequired.
What time is it, exactly?
 Each satellite carries around four atomic clocks, which use theoscillation of cesium and rubidium atoms to keep very accuratetime. How accurate are we talking about here? Well, your averageGPS atomic frequency standard has to maintain accuracy of plus/minusa second over more than 30,000 years. (That’s one part in 10 tothe 13th for you scientific types.) All satellites in the systemare synchronized at exactly the same time and it must be keptwithin 176 nanoseconds of UTC, plus accumulated jump seconds.Navigation messages from the SVs announce the difference betweenGPS time and UTC.
Each satellite carries around four atomic clocks, which use theoscillation of cesium and rubidium atoms to keep very accuratetime. How accurate are we talking about here? Well, your averageGPS atomic frequency standard has to maintain accuracy of plus/minusa second over more than 30,000 years. (That’s one part in 10 tothe 13th for you scientific types.) All satellites in the systemare synchronized at exactly the same time and it must be keptwithin 176 nanoseconds of UTC, plus accumulated jump seconds.Navigation messages from the SVs announce the difference betweenGPS time and UTC.
Okay, we have accurate clocks in the satellites. Now all we needare accurate clocks in the receivers, sync ’em up and we’re inbusiness. Of course, if your discount GPS receiver had to havea cesium clock, it’d cost about $200,000 and be about the sizeof a desktop computer. The way around that was to develop internalreceiver clocks that are consistently accurate over relativelyshort periods of time, as long as they’re reset often.
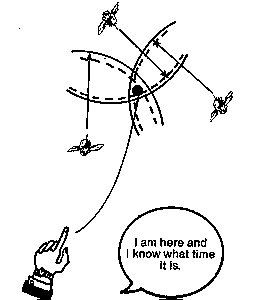
Here’s how the receiver clocks are reset: Remember how we explainedthat DME business, with three intersecting circles? Well, GPSdoes the same thing only it uses three intersecting spheres todetermine position.
Let’s for a moment assume that the receiver clock and satelliteclock are exactly in sync. The receiver times the signal, figuresthe distance from three satellites and where the three spheresintersect…voila…that’s our position. But, the receiver doesn’tknow for sure that its clock is perfectly synced up with the satellites.Remember, a lousy millionth of a second translates to a thousand-footerror.
So, just to be sure, the receiver listens for a fourth satellite.If the fourth line of position doesn’t pass through the otherthree, the receiver knows something is wrong; it’s geometricallyimpossible for four mutually intersecting spheres to merge atthe same point unless the clock is spot on. The receiver assumes,then, that because the fourth line doesn’t jive with the others,the receiver’s internal clock must be out of sync.
The receiver then runs a simple little routine to adjust the clockuntil all four lines of position intersect the same point. Thisis known as correcting clock bias and it’s how the receiver resetsits clock. That’s one of the things that’s going on when yourreceiver has just been turned on and you’re waiting for it toinitialize.
Breaking the code
 So much for the clock syncing. Pretty clever, eh? It gets better.
So much for the clock syncing. Pretty clever, eh? It gets better.
We said that in order to measure distance, the receiver has toknow exactly when the signal left the satellite. Just havinga clock set exactly to satellite time isn’t enough.
The receiver determines range using something called pseudo-randomcode. Think of the code as looking like the teeth on a carpenter’ssaw, with a few broken off at random points. Each satellite transmitsits own random code. The receiver has a code generator pre-programmedto generate the exact same codes (in 32 variations).
When the receiver hears a satellite, it matches up the code—likealigning the patterns of broken teeth on two saws. Since it knowsthat the signal carrying the code left the satellite at a certainexact time, all the receiver does is generate its matching codeat exactly the same time. It then measures how long ittakes the random code from the satellite to arrive and…right…itconverts this time lapse to a distance measurement. It does thisfor four satellites and the rest is simply math.
Earlier, we said four satellites are necessary, with the fourthrequired to sync the clock and three others for lines of position.Actually, if the receiver operator knows his altitude, he canplug that into the receiver and that serves as one lineof position. Then, only two other SV ranges are required to determineposition. The third satellite is used to sync the clock. Thisis known as two-dimensional navigation.
Hey, can you hear me?
There’s another important reason for random code; it relates tosome basic GPS design limitations. In order to be affordable,GPS satellites had to be relatively small and light—the BlockII production SVs weigh just less than 2,000 pounds. That meansthat power requirements are limited and the radiated signal poweris also quite low, on the order of 40 watts.
Think about that. There’s a 40-watt transmitter floating out therealmost 11,000 miles away and it has to blanket a very large portionof the earth’s surface with a receivable signal. Big problem.
For comparison, a typical communication satellite has much morepower and it radiates a very directional signal that you needa satellite dish to receive. For obvious reasons, ships, planes,cars and other moving vehicles, can’t have dishes. Who wants aplane that looks like a West Virginia sharecropper’s double-widetrailer? Besides, they’d blow off in the slipstream.
Rather than directing a high power signal, then, a GPS satellitespreads a very low power signal over a large area. It’s so low-poweredthat it’s completely hidden in the background hash of cosmic rays,car ignitions, neon lighting, computer drive fuzz and so forth.That’s where random code comes in.
The receiver starts generating its own code and listening formatches in the background noise. Once it has enough matches torecognize the SV’s transmission, it drags the signal out of backgroundmuck and "locks on." When three SVs are locked up, navigationcan begin.
This is why a receiver can get by with a very small, relativelynondirectional antenna. Handheld GPS units have antennas thatare only a couple of inches square or perhaps about the size ofa cigar. One other thing: using pseudo-random code and low, lowpower makes it very hard to jam a GPS signal. For military purposes,this is obviously very desirable.
A big system
 That’s the theory. It works. It works very well, as a matterof fact. But it takes a whole lot of effort and money to keepit working.
That’s the theory. It works. It works very well, as a matterof fact. But it takes a whole lot of effort and money to keepit working.
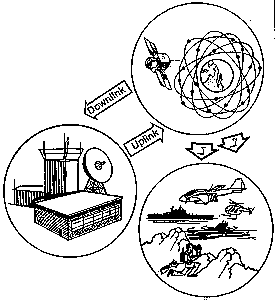
The GPS system consists of three major parts—the user segment(that’s us), the ground or control segment (the DOD nerds whorun the thing) and the space segment. The space segment is composedof 24 satellites, 21 active SVs and 3 in-orbit spares.
Boys in Blue
The U.S. Air Force’s 2nd Satellite Operations Squadron at FalconAFB in Colorado maintains the GPS system. These guys are the groundsegment. They have monitoring stations at several points on theglobe, from which they keep track of satellite health, maintenanceand so forth.
Make no mistake about it, GPS is a high maintenance system.The satellites require regular tweaking including data uploads,orbital positioning adjustments and clock maintenance. If theground segment stopped doing this constant maintenance, it’s saidthat the system would "gracefully degrade" to completeuselessness in about two weeks time.
So, as each satellite whizzes along and completes one earth orbitevery 12 hours, the Boys in Blue from Falcon talk to it everyfew hours. Communications are uplinked in S-band at 2227.5 Mhzand confirming messages are downlinked on 1783 mHz. What do theground guys tell the satellites?
Well, we mentioned basic maintenance items, including clock commands,power and attitude messages, new programming instructions. Occasionally,the SV must undergo what’s called a "momentum dump."Each SV has a series of gyroscopic wheels for stabilization. Inspace, these wheels tend to accelerate and would do so indefinitely,eventually disintegrating. By dumping the wheel energy periodically,this unpleasant scenario is avoided.
Orbital perturbations
Most of the uploading relates to routine navigation data, includingalmanac and ephemeris information. Probably the most importantis the ephemeris, which compensates for the SVs normal orbitalperturbations.
As it circles the earth, each satellite is subject to severalmajor influences which cause its orbit to be less than perfectlycircular. The major influence is the earth’s equatorial bulgebut solar wind and other effects also take a toll. The GPS orbitalperturbations are defined by 16 constants and these are updatedand uploaded at least once a day (maybe more often) along withclock correction data. The satellite then rebroadcasts this andyour receiver decodes it as ephemeris data. The ephemeris tellsthe receiver exactly where the satellite is in space so,when the receiver calculates distance, it’ll know exactlywhere the source of the signal is; each SV broadcasts its ownephemeris data.
In addition, each SV also broadcasts what’s called an almanac.In more general terms than does the ephemeris, the almanac tellsthe receiver the location of all of the SVs in the GPSconstellation. This lets the receiver know when and where to lookfor satellites, as it’s attempting to establish a fix. Your receiverstores an almanac in its memory and that data is constantly updatedwhen the receiver is tracking satellites. If the receiver is turnedoff for several months, the almanac will usually remain usableenough for the receiver to find satellites and upload a new almanac.
Bit by bit
Of course, all this data we’ve been blithely describing here hasto find its way through 10,900 miles of space and into your receiver’scomputer memory. This is another one of GPS’s elegant design features.
Remember how we explained that a communication satellite usesa relatively high powered, directional signal? Such a signal allowsfor a rather dense data stream, which, when you think about it,is just what a multi-channel comm satellite needs. Lottsa phonecalls, fax bits, video pixels and so on streaming down from space.The GPS data stream is just the opposite; very little informationspread out over a wide, non-directional signal. If satellite signalswere soup, a comm bird would be a rich, thick minestrone, GPSwould be chicken broth, and a pretty thin one at that.
The GPS data stream trickles down from each SV in 1500-bit frames,each composed of five subframes 300 bits long. Subframes 4 and5 are subcommutated 25 times each, which is a fancy way of sayingthat to get a complete data message, requires that 25 full framesbe sent. A full 1500-bit frame takes 30 seconds to send. Do themath here and you’ll realize that the GPS data rate is slowerthan slow—it’s 50 baud. If your computer downloaded this articleat 50 baud, it would take about six hours. You could read thedamn thing c-h-a-r-a-c-t-e-r by c-h-a-r-a-c-t-e-r.
The data subframes contain various information. Subframes 1,2and 3 contain time and date information, user range accuracy,satellite health status messages, clock correction, ephemerisdata and some other odds and ends. Subframes 4 and 5 contain thealmanac, which, as we noted, is the location in space of allof the satellites. It’s a fair amount of data and that’s why it’ssubcommutated. If it weren’t and the almanac were transmittedcontinuously until complete, a GPS receiver would take about 12minutes to initialize, every time you turned it on. Oh…and nonavigating while you’re waiting.
What it’s doing
So you just bought a brand new Garmin or Trimble. You take itout of the box, turn it on and it doesn’t work. You read the instructionsand learn that it needs a current almanac if one wasn’t downloadedwithin the past nine months or so or if the receiver was movedmore than a 1,000 miles.
You go outside, turn it on and it just sits there. What’s it doing?
Well, for one thing, it’s looking for a satellite so it can graban almanac, which it must have in order to find the three or foursatellites it needs to fix position. If the receiver is "dumb"and has no almanac at all or an outdated almanac, it’ll take 121/2 minutes to download. Why?
Well, remember, the almanac is in subframes 4 and 5, each of whichtakes 6 seconds to send. Because there are five subframes, though,almanac is coming through only 2/5ths of the time. It takes 25full data frames to get a full almanac. Each full frame takes30 seconds so 25 frames takes 12 1/2 minutes, which is why yourreceiver manual gives 12 1/2 minutes as the download time.
Oh, in case you’re wondering, here’s what an almanac (or at leasta portion of one) looks like:
| Epoch: 48871.0000 MJD (almanac reference time 9-6-1992 0h UTC) ID# Type smaxis(km) eccentri inclina rt.ascen arg.peri mean-ano Hlth 2 GP 26560.0520 0.011080 54.9026 342.9035 194.5554 224.6108 0 |
Got that? Once the receiver’s got it, it can locate other SVsin the sky, download the ephemeris and other data and tell youwhere you are, within a few feet or so.
How accurate, anyway?
Which brings us to the question of accuracy. You hear all kindsof incredible claims about GPS being accurate enough to locatea gnat’s ass while others say its only good for about 100 meters,give or take. Which is true? Well, it depends.
GPS is generally said to be available in two forms, PPS and SPS.Depending on whose figures you want to believe, PPS or precisionpostioning service is accurate to about 29 meters with single-frequencyreceivers. SPS or standard positioning service is actually capableof the same accuracy except…the DOD invokes something calledselective availability. SA is currently on and that degrades theSPS accuracy to about 100 meters. GPS usually delivers on thatpromise, too.
SA, by the way, is an intentional "dithering" of theclock accuracy and perhaps a contamination of the ephemeris data.Why the DOD thinks this makes any difference to a potential enemyis beyond us.
Anumber of factors go into making that 100-meter potential error.Break these factors down and they might look like this:
SV clock errors= 2 feet
Receiver errors= 4 feet
Empemeris errors = 2 feet
Ionospheric errors = 12 feet
SA errors = 25 feet
Throw in the statistical average and the ability to repeat a fixreliably over and over and the error gets up around 300 feet orso, with SA on. With SA off, it’s around 60 to 200 feet.
One last note about errors: We mentioned something called a singlefrequencyreceiver. That’s a bit confusing because we didn’t explain thatGPS satellites broadcast on two frequencies, called L1 and L2.L1 is at 1575 mHz, L2 is 1227 mHz. Military receivers generallyreceive both L1 and L2. They compare the results from each anduse this information to greatly reduce the ionospheric errorsGPS signal are subject to when passing through the atmosphere.Single frequency receivers—our Garmins and Trimbles—use a fixedmathematical model to allow for iono errors.
That’s it!
So, that’s how GPS works. Take it from us, a buncha cynical andhardbitten journalists who’ve seen it all, this is hot stuff.The people who designed this system were smart and clever andhave created a fantastic navigation system. No kidding.
Like the Pepsi ads say, you gotta have it!


































